Consistency Models is a popular approach to reduce Stable Diffusion required steps from 30-50 steps to 1-8 steps without sacrifices much of quality image. In reality, you can easily apply Consistency Models to any community base models by attach a LoRA to the model, without any retraining. However, when deep dive into the paper, there are many terminology that cause me somewhat confusing and cause a lot of trouble to grab the concept thoroughly.
This post is an attempt of me breaking down some terminology that will encounter frequently in Consistency Models. Hoping it would provide some knowledge to understand how could this technique successfully reduce steps in Stable Diffusion models.
Stable Diffusion theory
In short, Stable Diffusion start from a random noisy image and gradually denoising it according to text prompt provided. Which best illustrated with the image below

According to DDPM1, image generation sampling is defined as
\[\begin{equation} \label{eq1} \tag{1} \mathbf{x_{t-1}} = \frac{1}{\sqrt{\alpha_t}}\Bigl(\mathbf{x_t} - \frac{1- \alpha_t}{\sqrt{1 -\bar{\alpha_t}}}\boldsymbol{\epsilon_\theta}(\mathbf{x_t}, t)\Bigl) + \sigma_t\mathbf{z} \end{equation}\]In the above equation, \(\mathbf{x_t}\) is the “image” at timestep \(t\), model prediction \(\boldsymbol{\epsilon_\theta}\) and \(\mathbf{z}\sim \mathcal{N}(\mathbf{0},\,\mathbf{I})\). We can see that the next denoised image is generated by moving the original image by the model prediction with addition of some noise. Later method, DDIM2 is a speed up version of this sampling process and being used more often than DDPM sampling. However, a random noise still need to be injected in the procedure.
Stochastic differential equations (SDE)
Stochastic differential equations (SDE) are equations calculating the rate of change of a variable depending on the rate of change of some input variables but with some randomness in the equation (hence the name stochastic). Remove the stochasticity, we got Ordinary differential equation (ODE)
A common ODE that we meet in life is the bank interest rate \(dx = 0.04xdt\), where \(x\) is the amount in bank account and \(t\) is the time in year unit.
Another example of SDE is the diffusion process in Stable Diffusion which convert data to noise, called Forward SDE. In [3], it is formally defined as
\[\begin{equation}\label{eq2}\tag{2} d\mathbf{x} = f(\mathbf{x}, t)dt + g(t)d\mathbf{w} \end{equation}\]where \(f(\mathbf{x}, t)\) is the drift function and \(g(t)\) is a scalar multiplier for Brownian motion \(\mathbf{w}\) (or random noise \(\mathbf{z}\)). If we set \(f(\mathbf{x}, t)=0\), we got the standard diffusion.
How about the reverse?
Actually, with some rearrange, equation \(\eqref{eq1}\) is a differential equation itself which hold the form
\[\begin{equation}\label{eq3}\tag{3} d\mathbf{x} = \boldsymbol{\epsilon'_\theta}(\mathbf{x}, t)dt + g(t)d\mathbf{w} \end{equation}\]called Reverse SDE. However, with mathematical analysis, there is a more precise equation to reverse the process of \(\eqref{eq2}\)
\[\begin{equation}\label{eq4}\tag{4} d\mathbf{x} = [f(\mathbf{x}, t) - g^2(t)\nabla_x log\ p_t(x)]dt + g(t)d\mathbf{w} \end{equation}\]\(\nabla_x log\ p_t(x)\) is now the model prediction that we use to denoise the image \(\nabla_x log\ p_t(x) \approx \boldsymbol{\epsilon_\theta}(\mathbf{x_t}, t)\). This is interesting because \(\nabla_x log\ p_t(x)\) is the score function (gradient of log likelihood) of probability distribution \(p_t(x)\), hence the reason why sometimes Stable Diffusion is also referred as score models in literatures.
This sampling process is totally non-deterministic (hence the name) so it would be impossible to know the final destination given the original noise \(\mathbf{x_T} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\). Unless, it is…
Probability Flow - Ordinary differential equation (PF-ODE)
In a research paper3, Song et al. show that it is possible to convert SDE from diffusion sampling process into an ODE, called Probability Flow ODE (PF-ODE).
\[\begin{equation}\label{eq5}\tag{5} d\mathbf{x} = [f(\mathbf{x}, t) - \frac{1}{2}g^2(t)\nabla_x log\ p_t(x)]dt \end{equation}\]Not much changes from \(\eqref{eq4}\) except that now there is no random involved. In other words, there is a way to know how \(\eqref{eq1}\) would end without going through multiple steps (30-50 steps to be specific).
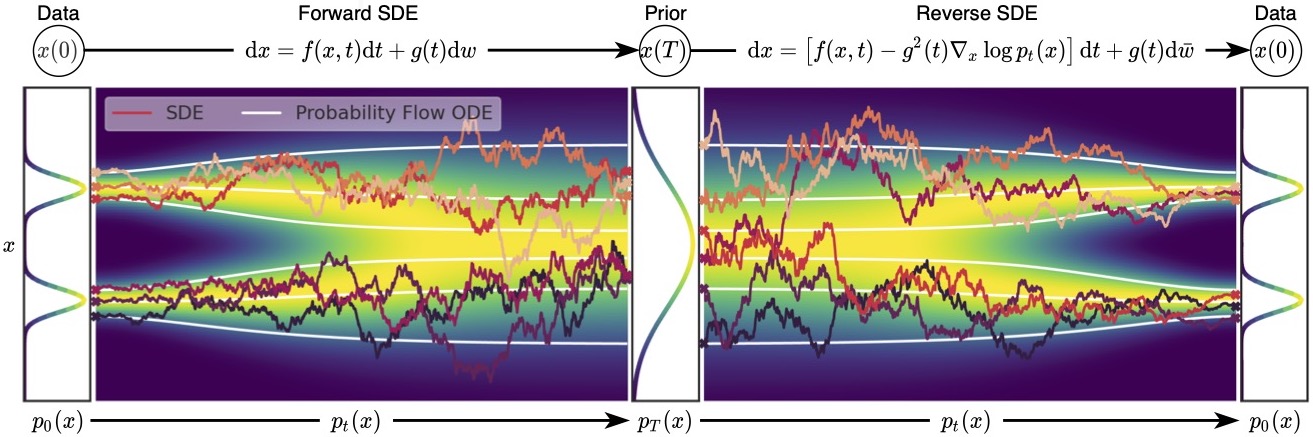
In the image above, as we can see the trajectory of Forward SDE converting data to noise and Reverse SDE convert them back. Note how PF-ODE correctly smoothen out the trajectory of both and converge back to the correct data distribution. As we understand the concept of SDE and PF-ODE, navigating through Consistency Models4 would be easier to understand.
Final Thought
With SDE and PF-ODE, we got a different perspective to formulate sampling process of denoising a sample. These concept is important as it will be mentioned in later researches that utilize consistency method to distill step in diffusion models like LCM-LoRA, TCD or HyperSD
References
[1] Denoising Diffusion Probabilistic Models
[2] Denoising Diffusion Implicit Models
[3] Score-Based Generative Modeling through Stochastic Differential Equations
[5] https://yang-song.net/blog/2021/score
[6] https://lilianweng.github.io/posts/2021-07-11-diffusion-models